2023. 10. 1. 17:49ㆍSWU_1학년 2학기/현대 암호학 기초
3주차는 고전암호학을 학습할 것이다.
목차는 다음과 같다.
시저 암호 (시프트 암호)
아핀 암호
단일 치환 암호
다중 치환 암호
전치 암호
암호 알고리즘 안전성 원칙
📌시저 암호 (Caesar Cipher)
카이사르 암호(Caesar cipher) 또는 시저 암호는 암호학에서 다루는 간단한 치환암호의 일종이다.
실제로 로마의 황제 카이사르는 이 카이사르 암호를 사용하기도 했다.
카이사르 암호는 암호화하고자 하는 내용을 알파벳별로 일정한 거리만큼 밀어서 다른 알파벳으로 치환하는 방식이다.
예를 들어 3글자씩 밀어내는 카이사르 암호로 'COME TO ROME'을 암호화하면 'FRPH WR URPH'가 된다. 여기서 밀어내는 글자 수는 암호를 보내는 사람과 함께 정해 더 어려운 암호를 만들 수 있다.
이런 카이사르 암호는 순환암호라고 한다.
- 평문 및 암호문 공간
- 알파벳으로 구성되어있다.
- 시프트 암호 (Shift Cipher)
- 알고리즘 - 평문 알파벳 별로 일정한 문자 수 만큼 평행이동
- 키 - 평행이동 거리
예를들어 암호화키가 3인경우 a는 d로 3개 문자만큼 평행이동한다.
hello는 각각 khoor로 암호화된다.
키 개수는 알파벳 개수만큼 총 26개이다.(아무 것도 하지 않는 것 포함, 매우 작다)
전사 공격 (brute - force attack)
전수 조사/탐색 (exhaustive search)
0~25 까지 각각의 키에 대해 복호화를 수행 → 의미가 있는 평문으로 해독되는 경우 키 발견
➡️ 참고하기
기원전 100년경에 로마의 장군 카이사르가 썼던 암호로, 시저 암호, 카이사르 암호라고 불린다.
그 당시 '암살자를 조심하라 Be careful for assassinator'라는 암호문을 전달하기 위해 사용되었다고 한다.
이 암호는 평문에서 사용되고 있는 알파벳을 암호키 k개만큼 평행이동시켜 암호화하는 '치환 암호'이다.
간단한 방법으로 암호화하기 때문에 암호키만 알게 되면 쉽게 암호를 복호화(암호를 해독하는 것) 할 수 있다는 단점이 있다.
알파벳을 평행이동시키는 작업 자체가 암호화 알고리즘이라고 할 수 있다.
예를 들어, 평문 Kabsoonyee가 있으며, 카이사르 암호에 사용되는 암호키는 3이라고 가정하자.
암호키는 3이므로 알파벳을 3문자 평행이동시킨다. 평행이동시킨 문자에 의해서 평문을 암호화 하면 NDEVRRQBHH이다.
[ 출처 : 네이버 지식백과] 카이사르 암호
📌아핀 암호(Affine Cipher)
하나의 키를 이용하여 덧셈의 방식으로 알파벳을 옮기는 이동암호는 노출되기 쉽기 때문에, 이어서 등장한 것이 곱셈과 덧셈을 결합하여 암호화하는 ‘아핀암호(affine cipher)’이다.
시저 암호(시프트 암호)를 일반화
- 각 알파벳을 다른 알파벳으로 치환
✅ 알파벳을 숫자로 생각하기
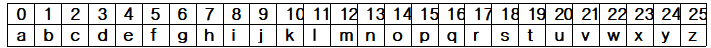
- 알파벳 위에서 연산(덧셈, 곱셈)
- b+d = 1 + 3 = 4 = e
- i+x = 8 + 23 = 31 → (26으로 나누었을때 나머지, mod 26 연산) → 5 = f
- e x g = 4 x 6 = 24 = y
- d x j = 3 x 9 = 27 = 1 mod 26 = b
- 곱셈에 대한 역원
- d x j = 3 x 9 = 27 = 1 mod 26 → d와 j는 서로가 곱셈에 대한 역원이다.
- 3^-1 = 9, 9^-1 = 3 mod 26
- 26과 서로소인 숫자는 모두 역원을 가진다.
- 암호화 키
- 26과 서로소인 숫자 𝛼
- 평행이동 거리 숫자 𝛽
- 암호화 알고리즘
- 메시지 𝑥를 아래와 같이 치환한 𝑦를 계산
- 𝑦 = 𝛼 ⋅ 𝑥 + 𝛽 𝑚𝑜𝑑 26 (일차 함수 꼴)
- 즉, 시프트 암호에서 곱셈을 추가한 것
- 복호화 알고리즘
- 𝑥 = 𝛼 ^−1 ⋅ y − ʙ 𝑚𝑜𝑑 26
- 예시
- 𝛼 = 3, 𝛽 = 2
- (암호화) 메시지 𝑥: = 𝑒 = 4 ⇒ 3 × 4 + 2 = 14 𝑚𝑜𝑑 26 = 𝑜
- (복호화) 암호문 𝑜 ⇒ 14 − 2 × 3 −1 = 12 × 9 = 108 = 4 𝑚𝑜𝑑 26 = 𝑒
📌 치환 암호
주어진 문자들의 순서만 바꾸는 전치암호와 달리 ‘치환암호(substitution cipher)’는 각 문자를 다른 문자로 바꾸는 암호화 방식이다.
치환암호에는 하나의 문자가 다른 하나의 문자로 바뀌는 ‘단일치환암호(monoalphabetic substitution cipher)’와 하나의 문자가 여러 개의 문자로 바뀌는 ‘다중치환암호(polyalphabetic substitution cipher)’가 있다.
출처 : [네이버 지식백과] 치환암호
단일 치환 암호 (Monoalphabetic Substitution Cipher)

- 암호화 키로 가능한 모든 일대일 대응을 고려
- 키의 개수 = 26! ≈ 4 × 1026 ≈ 2 95
- 매우 많음
- 약 13자리 비밀번호 개수에 대응
- 영문자 대 (26), 영문자 소 (26), 숫자 (10), 특수문자 (32) → 약 100개
- 여전히 안전하지 않았다.
- 단일 치환 암호에서 같은 문자는 항상 같은 문자로 변환 (deterministic)
- 암호 해독은 다양한 부가 정보를 이용할 수 있다 ( 즉 , 빈도 분석이 가능하다. )
- 영어 알파벳의 출현 빈도를 활용하여 의미론적 추측이 가능하다는 단점이 있다.
다중 치환 암호 (Polyalphabetic Substitution Cipher)
- 단일 치환 암호 약점
- 같은 문자는 항상 같은 문자로 변환 → 빈도 분석에 취약
- 같은 문자가 다른 문자로도 암호화되는 성질이 필요하다.
✅ 비즈네르 암호 (Vegenere Cipher)
프랑스의 외교관인 블레즈 드 비즈네르(Blaise de Vigenere)에 의해 만들어진 것으로, 트리테미우스 암호를 한 단계 더 발전시킨 암호 방법이다.
트리테미우스 암호에 쓰이는 26x26 암호표를 동일하게 사용하지만, 암호화하는 과정에서 한 단계를 추가적으로 사용함으로써 좀 더 어려운 방법으로 암호화하는 방식이다.
시저 암호, 트리테미우스 암호와 유사하게 치환 방식을 사용하지만, 단일 치환이 아닌 다중 단일 문자 치환 방식을 사용한다. 트리테미우스 암호에서 평문을 암호화 할 때에 i번째의 문자는 i번째 줄에 있는 암호문을 적용한다는 규칙에서 벗어나, 단순히 동일한 줄에 있는 암호문을 사용하지 않고 주어진 암호화 키에 의해 매 문자마다 새로운 규칙을 정해서 암호화한다
출처 :[네이버 지식백과] 비즈네르 암호 [Vigenère cipher]
➡️ 암호화 키
- 블록 크기 𝑚 (모든 자연수가 가능)
- 일대일 대응 𝑓: = (𝑘1, 𝑘2, … , 𝑘𝑚)
- 블록내 첫번째 문자는 𝑘1 만큼 shift, 두번째 문자는 𝑘2 만큼 shift, …
- 26𝑚 가지 키가 존재 (𝑚 = 20 ⇒ 약 2 ^ 95 개)
비즈네르 암호
프랑스의 외교관인 블레즈 드 비즈네르(Blaise de Vigenere)에 의해 만들어진 것으로, 트리테미우스 암호를 한 단계 더 발전시킨 암호 방법이다. 트리테미우스 암호에 쓰이는 26x26 암호표를 동일하게
terms.naver.com

VISE NERE를 암호화해보자.
- 𝑚 = 4, 𝑓: = (21,4,2,19)
- 평문 : “VISENERE”
m이 4이므로 4개로 나누어 각각 21, 4, 2, 19 를 이용하여 암호화한다.
V I S E 는 21, 4 , 2 ,19 에 의해
✅ 힐 암호 (Hill Cipher)
행렬은 암호에도 이용된다. 대칭적인 키를 갖는 암호로, 1929년 레스터 힐(Lester Hill)에 의해 제안된 ‘힐 암호(Hill cipher)’는 역행렬이 존재하는 정사각행렬을 이용하여 암호화한다.
- Lester Hill 이 1929년에 발명되었다.
- 알파벳 위의 덧셈, 곱셈 연산
- 𝑏 + 𝑑 = 1 + 3 = 4 = 𝑒
- 𝑖 + 𝑥 = 8 + 23 = 31 → (26으로 나누었을 때 나머지, mod 26 연산) → 5 = 𝑒
- 4 × 6 = 24 = 𝑦
- 7 × 20 = 140 = 10 = 𝑘
- 비즈네르 암호에서 일대일 대을은 행렬 M 곱하기로 바꾼 것이다.
- 암호화 키
- 파라미터 𝑚
- 𝑚 × 𝑚 행렬 𝑀
- 단, 26으로 나누어 나머지를 취하는 연산에 대해 역행렬 𝑀^−1가 존재해야 한다.
힐 암호화를 해보자.
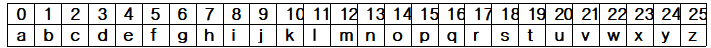
📌 전치 암호
평문의 문자를 각종 암호 방식을 사용하여 다른 문자로 바꾸는 치환형 방식이 아니라, 평문의 문자 위치만을 바꾸는 방식이다.
- 암호화 방식
- 평문의 알파벳 순서를 재배치하는 방식으로 암호화
- (평문) A B C D E → (암호문) B A D C E
- 키
- 길이 m의 문자열을 섞는 방식
| 이동 전 위치 | 1 | 2 | 3 | 4 | 5 |
| 이동 후 위치 | 2 | 1 | 4 | 3 | 5 |
- 키 공간 크기
- {1, … , 𝑚} 에서 {1, … , 𝑚} 으로 가는 모든 일대일 대응의 개수 = 𝑚!
📌 에니그마
에니그마(독일어: Enigma)는 회전자로 작동하는 암호 기계의 한 종류로, 그 이름은 고대 그리스어로 '수수께끼'를 뜻하는 아이니그마(고대 그리스어: αἴνιγμα)라는 말에서 따온 것이다.
암호의 작성과 해독이 가능하며 보안성에 따라 여러 모델이 있다.
1918년 독일인 아르투르 슈르비우스에 의해 처음 고안되어 상업적 목적으로 사용되었다.
특히 제2차 세계 대전 중 나치 독일이 군기밀을 암호화하는 데 사용하였다.
오랫동안 난공불락으로 여겨졌으나 전쟁 시작도 전에, 폴란드의 암호국, 비우로 시프루프 (Bioro Szyfrów)에서 해독의 기초를 마련하였다.
이들은 이후 영국과 프랑스의 암호학자들과 정보를 공유했고, 영국의 블레츨리 파크(Bletchley Park)의 암호학자들에 의해 해독되어 전쟁 중 연합군의 전략에 상당한 도움을 주었다.
에니그마는 1945년 독일 패전과 함께 사용이 중지됐지만, 형태가 변형되어 1970년대까지 주로 상업적 보안통신용으로 사용되었다. 에니그마를 원형으로 한 군용 보안통신기 역시 1960년대까지 사용되었다.
출처 : 위키백과
- 슈르비우스 (Scherbius)가 1918년에 고안
- 다중 치환 암호 (서브루틴으로 여러 종류의 단일 치환 암호를 혼합 사용)
- 전용 장비를 사용한 최초의 암호 시스템
- 2차 세계대전 독일군이 사용
- 해독
- 1930년대에 폴란드 암호국의 암호학자 Rejewski, Zygalski, Rozycki 등에 의해 초기 버전 해독
- 독일이 폴란드를 침공하기 2달 전에 영국으로 해독 기법이 전해짐
- 영국의 블레츨리 파크(Bletchley Park)의 암호학자들에 의해 해독 (튜링)
- Turing이 해독 장비 봄브(Bombe)를 제작
- Flowers가 Colossus 제작 (최초의 컴퓨터로 알려짐)
- 블레츨리 파크 그룹에 의해 에니그마가 해독되었다는 사실은 1970년대에 비로소 공개되었다.
➡️에니그마의 원리
- 플러그보드 (Plugboard)
- 단일 치환 암호
- 26개 알파벳 중 𝑛개를 골라 교차
- T → K, K → T
- 어떤 쌍을 선택하는지는 비밀 정보 (키)
- 매일 달라짐
- 별도 코드북을 통해 사전 전달
- 회전자 (Rotors)
- 각 회전자가 26개 알파벳 전체에 대한
- 단일 치환 암호
- 총 5개의 회전자
- 3개를 골라 순서에 따라 설치
- 회전체로써 어떤 값(알파벳)을 위쪽(시작 점)으로 설치하는가에 따라 치환 암호 키 가 달라짐
- 선택 회전자, 순서, 시작점은 모두 암호 키에 해당 (코드북으로 사전 공유)
- 키보드에 입력 후 오른쪽 회전자가 1/26 만큼 회전
- 오른쪽 회전자 한바퀴 회전 → 중간 회전 자 1/26 회전
- 중간 회전자 한바퀴 회전 → 왼쪽 회전자 1/26 회전
- 회전자 회전을 통해 하나의 알파벳이 여 러 개의 알파벳으로 치환 가능
- 각 회전자가 26개 알파벳 전체에 대한
- 반사경 (Reflector)
- 단일 치환 암호
- 26개 알파벳 전체에 대해 교차 (즉, 13개를 골라 교차 치환)
- 암호화과정
- 입력 ( T ) : 플러그 보드(K) > 오른쪽 회전자(U) > 중간 회전자(P) > 왼쪽 회전자(H)
- 출력 ( D ) : 왼쪽 회전자(G) > 중간 회전자(R) > 오른쪽 회전자(W)> 플러그보드(G)
에니그마 암호화 프로토콜
날짜별 키와 통신 키를 구분
| 날짜별 키 | 날짜별 선택 회전자 |
날짜별 회전자 결합 순서 |
날짜별 각 회전자 시작점 |
Enigma 장비를 제공하는 시점에 날짜별 설정이 기록된 코드북을 사전에 공유 |
| 통신 키 | 위와 동일 | 위와 동일 | 각 암호문별로 sender가 자체 설정 | • 날짜별 키로 sender의 시작점 키를 암호화하여 전달 • Receiver는 통신 키 암호문을 날짜별 키로 복호화하여 통신 키 복수 • 복구 통신 키로 각 암호문 복호화 수행 |
암호 안전성 원칙 (알고리즘과 키)
📌고전 암호 Summary
| 암호 | 암호화 알고리즘 | 키 |
| 시저 암호 | 평문의 각 문자를 일정한 문자 수 만큼 평행이동 | 미리 정한 문자 수 k |
| 단일 치환 암호 | 평문의 각 문자를 일대일 대응 함수에 따라 다른 문자로 치환 | 알파벳 간 일대일 대응 함수 |
| 전치 암호 | 평문의 각 문자의 위치를 permutation 함수에 따라 재배치 | permutation 함수 |
| 비즈네르 암호 | 평문의 각 문자를 위치 별로 정의된 문자 수 만큼 평행이동 | 위치 별 평행이동 거리 벡터 |
| 힐 암호 | 평문에 대해 행렬 M을 곱합 | 행렬 M (역행렬 존재) |
| 에니그마 | 에니그마 장비를 사용하여 암호화 | 플러그보드에 의한 치환 방식 3개 회전자 선택 및 순서 각 회전자 시작점 반사경에 의한 치환 방식 |
암호 알고리즘 안전성 원칙
- 암호 알고리즘을 비밀로 하면 안전할까?
- 새로운 암호 알고리즘을 사용하기 위해서는 매우 많은 안전성 분석이 수반되어야 한다
- 많은 사람들이 분석한 결과 안전하다고 판단된 알고리즘을 사용하는 것이 바람직하다.
- 케르크호프스의 원리 (Kerckhoffs principle)
- “키를 제외한 시스템의 다른 모든 내용이 알려지더라도 암호체계는 안전해야 한다.
- “적은 시스템을 알고 있다 (The enemy knows the system)”, 클로드 섀넌
- 많은 기기간 통신을 위해서는 암호 알고리즘의 표준화가 필요
- 암호의 안전성 = 키의 안전
'SWU_1학년 2학기 > 현대 암호학 기초' 카테고리의 다른 글
| 4주차_현대암호학 기초 (2) | 2023.10.08 |
|---|---|
| 3주차_ 현대암호학 기초 < 암호 안전성과 공격 모델 > (1) | 2023.10.01 |
| 2주차_현대암호학 기초 < 행렬 > (0) | 2023.09.26 |
| 2주차_현대암호학 기초 < 기초 정수론2 > (0) | 2023.09.23 |
| 1주차_현대암호학 기초 < 기초 정수론 > (0) | 2023.09.20 |