2023. 10. 8. 10:55ㆍSWU_1학년 2학기/현대 암호학 기초
오늘 학습할 내용은 다음과 같다.
비트 연산 & 선형 함수
일회용 패드 (One-Time Pad)
일회용 패드 안전성 (Perfect Secrecy)
블록 암호 (Block Cipher)
DES (Data Encryption Standard
📌 비트 연산 & 선형 함수
비트열이란?
0과 1로 표현된 수열 (이진수)을 말한다.
예) 01101101
어떤 수 𝑥가 𝑛 비트 ⇔ 𝑥 는 0과 1이 𝑛 개로 이루어진 수를 말한다.
예) 01101101 → 8 비트 숫자
𝑥 ∈ 0,1^ 𝑛 라고 쓰기도 함
1 비트: 비트열의 최소 단위 (0 또는 1)
1 바이트: 8-비트 비트열
컴퓨터는 모든 문자와 숫자를 비트열로 이해하고 처리
문자/숫자 입력 → 입력값 부호화 (encoding) → 연산 → 출력값 복호화 (decoding) -> 문자/숫자 출력
예) 아스키 코드

배타적 논리합
XOR (exclusive or)
- ⊕ 로 표시
비트 단위 XOR 규칙
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
즉, XOR 는 𝑚𝑜𝑑 2 연산과 같음
- 0 + 0 = 0 (𝑚𝑜𝑑 2)
- 0의 (𝑚𝑜𝑑 2) = 0
- 1 + 0 = 1 (𝑚𝑜𝑑 2)
- 1의 (𝑚𝑜𝑑 2) = 1
- 0 + 1 = 1 (𝑚𝑜𝑑 2)
- 1의 (𝑚𝑜𝑑 2) = 1
- 1 + 1 = 0 (𝑚𝑜𝑑 2)
- 2의 (𝑚𝑜𝑑 2) = 0
비트열 XOR
- 비트열 𝑥 ⊕ 비트열 𝑦
- 각 비트 단위로 XOR 연산을 수행

✔ 둘다 0이거나 둘다 1이면 즉 둘이 같으면 0으로 도출됨
둘이 같지 않다면 1로 도출됨
배타적 논리합 성질
[ 참고 ]
드림핵 Cryptography_배타적 논리합과 합동식 (tistory.com)
비트열 𝑥, 𝑦에 대해 일반적인 덧셈의 성질을 다 가진다.
- 𝑥 ⊕ 𝑦 = 𝑦 ⊕ 𝑥 (덧셈에 대한 교환법칙)
- (𝑥 ⊕ 𝑦) ⊕ 𝑧 = 𝑥 ⊕ ( 𝑦 ⊕ 𝑧 ) (덧셈에 대한 결합법칙)
- 𝑥 ⊕ 0 = 𝑥 (비트열 0이 덧셈에 대한 항등원)
자기 자신에 대한 ⊕는 0으로 이루어진 비트열이 된다.
- 즉, 덧셈에 대한 역원이 자기자신이다
- 비트 단위
- 0 ⊕ 0 = 0, 1 ⊕ 1 = 0
- 비트열 XOR
- 𝑥 ⊕ 𝑥 = 0

바이트
✅Byte
8 비트로 구성된 비트열 (10진수 0~255)
✅ Byte와 16진수
주로 4 비트 씩 끊어서 16 진수로 쓴다.

4비트 숫자는 10진수로 0 ~ 15
| 10진수 | 2진수 | 16진수 |
| 0 | 0000 0000 | 0x00 |
| 8 | 0000 10000 | 0x08 |
| 16 | 0001 0000 | 0x10 |
| 90 | 0101 1010 | 0x5A |
| 255 | 1111 1111 | 0xFF |
16진수로 썼다는 것을 표시하기 위해 비트열 앞쪽에 0x를 붙인다. (자명한 경우에는 생략 가능)
선형과 비선형
선형 함수 (Linear Function)
함수 𝑓: 𝑋 → 𝑌가 임의의 𝑥1, 𝑥2 에 대해, 𝑓 𝑥1 + 𝑥2 = 𝑓 𝑥1 + 𝑓(𝑥2) 을 만족
𝑥1 + 𝑥2 는 정의역 𝑋에서 정의된 연산
𝑓 𝑥1 + 𝑓(𝑥2) 는 공역 𝑌에서 정의된 연산
어떤 𝑥1, 𝑥2 에 대해 𝑓 𝑥1 + 𝑥2 ≠ 𝑓 𝑥1 + 𝑓(𝑥2) 이면, 𝑓 는 비선형 함수 (non-linear function)이다.
(예시) 바이트열과 XOR 연산
- 4 비트 숫자 𝑎 = (𝑎1, 𝑎2, 𝑎3, 𝑎4) 에 대해 순서를 섞는 함수 𝑓 𝑎 = 𝑎2, 𝑎3, 𝑎4, 𝑎1
- 임의의 𝑎 = (𝑎1, 𝑎2, 𝑎3, 𝑎4), 𝑏 = (𝑏1, 𝑏2, 𝑏3, 𝑏4) 에 대해 𝑓 𝑎 ⊕ 𝑏 = 𝑓 𝑎 ⊕ 𝑓 𝑏 가 성립
📌 일회용 패드 (One-Time Pad)
일회용 패드(One-Time Pad) 란?
- 버냄 (Vernam)이 1917년 고안했다.
- 냉전시기 미국과 러시아 (소련) 사이 hot line을 통한 통신 암호화에 사용하였다.
- 1940년대 섀넌(Shannon)에 의해 Perfect Secrecy (완전 안전성)을 가진다는 것이 증명되었다.
암호화
- 평문 비트열 𝑝 와 키 비트열 𝑘의 XOR 연산
- 𝑐 = 𝑝 ⊕ 𝑘
- 키 비트열 𝑘
- 평문 비트열 𝑝와 같은 길이
- Random 비트열
| 평문 (𝑝) | a | p | p | l | e |
| 아스키코드 |
01100001 | 01110000 | 01110000 | 01101100 | 01100101 |
⊕
| 키 (𝑘) | 01101011 | 11111010 | 01001000 | 01100101 | 00011100 |
⇓
| 암호문 (𝑐) | 00001010 | 10001010 | 00111000 | 00001001 | 0111001 |
복호화
- XOR는 자기자신이 덧셈에 대한 역원
- 𝑐 = 𝑝 ⊕ 𝑘 ⇒ 𝒑 = 𝒄 ⊕ 𝑘
| 평문 (𝑝) | a | p | p | l | e |
| 아스키코드 |
01100001 | 01110000 | 01110000 | 01101100 | 01100101 |
⇑
| 키 (𝑘) | 01101011 | 11111010 | 01001000 | 01100101 | 00011100 |
⊕
| 암호문 (𝑐) | 00001010 | 10001010 | 00111000 | 00001001 | 0111001 |
Perfect Secrecy
어떠한 공격으로도 평문에 대한 정보를 얻는 것이 불가능 (Perfect Secrecy) 하다.
| 암호문 (𝑐) | 00001010 | 10001010 | 00111000 | 00001001 | 0111001 |
< apple의 암호문 >
암호화 키 𝑘는 8 × 5 비트 숫자를 random하게 선택
임의의 단어 𝑝𝑖 에 대해서 유일한 키 𝑘𝑖 가 존재
𝑘𝑖 = 𝑐 ⊕ 𝑝𝑖
➔ 어떠한 단어도 같은 확률로 올바른 평문일 수 있다
➔ 암호문이 평문의 어떠한 정보도 포함하고 있지 않다 (암호문 자체가 그냥 random)
장점
- 매우 안전
- 빠른 암/복호화 연산을 지원 (가장 간단한 연산이 XOR만을 사용)
단점
- 키 배송 및 보관
- 앞으로 사용할 메시지 길이 만큼의 키를 사전에 공유하는 것이 필요
- 키 재사용 불가
- 키 동기화
- Sender와 Receiver 사이에 동기화가 어긋날 경우 복구할 방법이 없음
- 키 생성
- 대량의 예측불가능한 random을 생성하는 것이 어려움
📌 블록 암호
비즈네르 암호 (Vegenere Cipher)
암호화 키
- 블록 크기 𝑚 (모든 자연수가 가능)
- 일대일 대응 𝑓: = (𝑘1, 𝑘2, … , 𝑘𝑚)
- 블록내 첫번째 문자는 𝑘1 만큼 shift, 두번째 문자는 𝑘2 만큼 shift, …
- 26𝑚 가지 키가 존재 (𝑚 = 20 ⇒ 약 2 95 개)
힐 암호 (Hill Cipher)
비즈네르 암호에서 일대일 대응을 행렬 𝑴 곱하기로 바꾼 것
암호화 키
- 파라미터 𝑚
- 𝑚 × 𝑚 행렬 𝑀
- 단, 26으로 나누어 나머지를 취하는 연산에 대해 역행렬 𝑀^−1가 존재해야한다.
블록 암호
비즈네르 암호 & 힐 암호
- 평문을 블록화
- 개별 블록에 대해 암호화
위와 같은 형태의 암호화 알고리즘 종류를 블록 암호라고 함
이상적인 블록 암호
블록 암호
- 𝑚 − 비트 평문들의 집합에 대한 permutation (암호화 키) 으로 이해할 수 있음
- 𝑚 비트 블록 집합의 크기 = 0과 1을 𝑚개 나열하는 경우의수 = 2 𝑚
- {0,1}^ 𝑚 에서 {0,1}^ 𝑚로 가는 permutation 전체의 개수 = 암호화 키 공간 크기 = (2^𝑚)!
- 이상적인 블록암호는 (2 𝑚)! 개 전체에서 암호화 키를 random 하게 뽑는 것
- 키를 표현하는데 필요한 비트수 = log2(2^𝑚!) > 2 ^𝑚
- 𝑚 = 40 → 2 ^ 40 비트가 넘는 키가 필요 (4 GB) → 너무 크다
- 상용 블록 암호는 permutation 전체 집합에서 극히 일부만을 사용
- DES, AES 등
현실적 & 안전한 블록 암호
Shannon
- 1945, “A Mathematical Theory of Cryptography”
- 블록 암호 디자인을 위한 principle 제시
- Confusion – Diffusion Paradigm
Confusion (혼돈)
- 목적 - 키와 암호문과의 관계 감추기
- 암호문의 각 자리(bit)가 키의 여러 부분(bits)들로부터 영향을 받게
- 키에서 1 비트만 바뀌어도 암호문의 많은 부분들이 영향을 받음
Diffusion (확산)
- 목적 - 평문와 암호문과의 관계 감추기
- 평문에서 1 비트만 바뀌어도 암호문의 반 정도가 영향을 받게
- 암호문에서 1 비트만 바뀌어도 평문의 반 정도가 영향을 받게
블록 암호 알고리즘 구조
블록별 암호화 구조
- Confusion 과 Diffusion 의 결합으로 Round를 구성
- Round를 반복 (Iteration)

블록 암호는 2개의 기본 구조를 가짐
- Feistel Network
- DES의 기본 구조
- Substitution-Permutation Network
- AES의 기본 구조
📌 DES
Feistel Network
Feistel system
- Horst Feistel
- IBM 암호팀의 멤버
암호 알고리즘 LUCIFER를 개발
Feistel network, Feistel structure, Feistel cipher 등으로 불림
암호화의 기본 모듈(라운드)를 여러 번 반복해서 수행

✅ Feistel Network 입력부
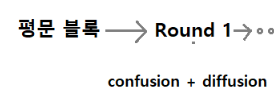
⇧
입력 평문
2ℓ − bit 블록
입력 평문을 반으로 나눔
𝐿0: 왼쪽 ℓ − bit 블록
𝑅0: 오른쪽 ℓ − bit 블록
이후 왼쪽과 오른쪽 ℓ −bit 각각에 대해 연산을 수행
✅ Feistel Network 𝒊번째 라운드

⇧
라운드 키 (𝑘𝑖)
각 라운드마다 라운드키를 가짐
라운드 함수 (𝐹)
라운드에 상관없이 일정한 함수 사용
비선형성을 제공하며 안전성 보장에 핵심적 역할
암호화 과정
(왼쪽) 𝐿𝑖 ← 𝑅𝑖−1
오른쪽 𝑅𝑖 ← 𝐿𝑖−1 ⊕ 𝐹𝑘𝑖 (𝑅𝑖−1)
✅ Feistel Network 마지막 라운드와 출력부
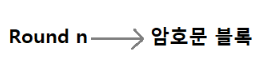
⇧
암호화 과정
마지막 라운드는 좌우를 바꾸는 과정 없음
𝐿𝑛 ← 𝑅𝑛−1
𝑅𝑛 ← 𝐿𝑛−1 ⊕ 𝐹𝑘𝑛 (𝑅𝑛−1)
출력부
왼쪽과 오른쪽을 연결 → 2ℓ − bit 암호문 출력
✅ Feistel Network 복호화
암호화와 같은 구조로 복호화를 진행
라운드키만 역순으로 입력하여 암호화 과정과 똑같 이 진행함
1라운드 Feistel Network 예시
암호화
𝐿1 ← 𝑅0 • 𝑅1 ← 𝐿0 ⊕ 𝐹𝑘1 (𝑅0)
복호화
𝑅1 ⊕ 𝐹𝑘1 𝐿1 = 𝐿0 ⊕ 𝐹𝑘1 𝑅0 ⊕ 𝐹𝑘1 𝑅0 = 𝐿0
𝐿1 = 𝑅0
✅ Feistel Network 특징
원하는 만큼 라운드 수를 늘릴 수 있다.
라운드 함수 𝐹는 어떤 것을 써도 복호화가 된다
- Feistel network의 복호화는 𝐹 의 역함수를 몰라도 된다
- 원하는 만큼 복잡한 𝐹 를 역함수 계산가능성 고려없이 만들면 된다
암호화 구조 = 복호화 구조
- 하드웨어 구현에 적합
DES 개요
DES (Data Encryption Standard)
- 1973년 미국 NBS(현재의 NIST)가 암호 알고리즘 표준화 작업을 진행
- 1974년 IBM에서 LUCIFER를 제출
- NSA (미국 국가안보국) 에서 검토, 수정을 거쳐 1974년 DES를 표준으로 채택
- NSA의 design 관여로 초기부터 다양한 보안상 우려가 제기됨
DES 구조
𝐼𝑃
- Initial Permutation
- 64 비트 비트열의 순서를 섞는 permutation • 𝐼𝑃^ −1 :𝐼𝑃의역함수
- 암호학적으로 큰 의미는 없음
DES Challenge
- 컴퓨터 연산 능력 발달로 현재 DES는 짧은 시간에 전수 조사로 키를 얻을 수 있음
- 현재 DES 는 사용되고 있지 않으나, 몇몇 오래된 시스템에서는 호환성 문제로 사용되고 있음
- RSA 사에서 주관
- DES Challenge I (1997): 96일 by the DESCHALL Project
- DES Challenge II-1 (1998): 41일 by distributed.net
- DES Challenge II-2 (1998): 56일 by Deep Crack machine built by Electronic Frontier Foundation (EFF)
- DES Challenge III (1999): 22시간 15분 jointly by distributed.net and Deep Crack
'SWU_1학년 2학기 > 현대 암호학 기초' 카테고리의 다른 글
| 10주차_현대암호학 기초 [기초 대수학] (0) | 2023.11.14 |
|---|---|
| 9주차_현대암호학 기초 [ 블록 암호 모드(Mode of Operation) ] (0) | 2023.11.05 |
| 3주차_ 현대암호학 기초 < 암호 안전성과 공격 모델 > (1) | 2023.10.01 |
| 3주차_현대암호학 기초 < 고전 암호 > (2) | 2023.10.01 |
| 2주차_현대암호학 기초 < 행렬 > (0) | 2023.09.26 |