2023. 11. 19. 00:07ㆍSWU_1학년 2학기/현대 암호학 기초
공개키 암호 & RSA 암호
RSA 암호 안전성
📌 RSA 암호
공개키 암호
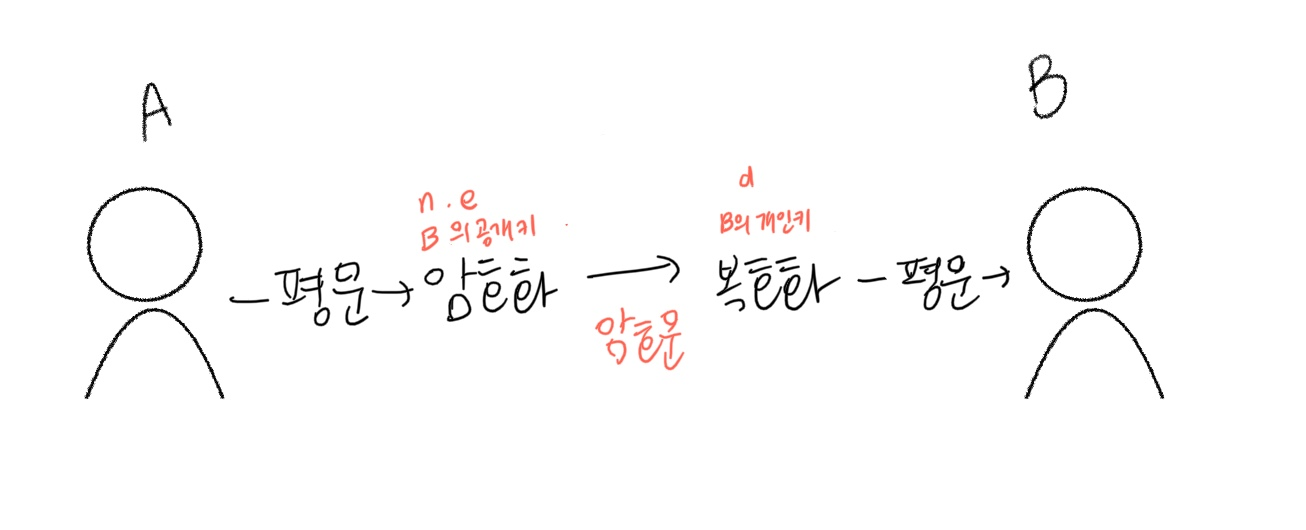
- 공개키 암호 (Asymmetric Key Encryption, Public Key Encryption)
- 암호화 키와 복호화 키가 다르다.

- 암호화 방식
- B가 자신의 공개키 (암호화 키)를 공개
- A는 B의 공개키로 암호문 생성
- B이 자신의 개인키 (복호화 키)로 암호문 복호화
- B의 공개키로부터 B의 개인키를 알아내는 것이 어려워야한다.
- RSA, ElGamal, 타원곡선 암호 (ECC)
RSA 암호 개요
1978년 Ron Rivest, Adi Shamir, Leonard Adleman 이 발표
2002년 Turing Award 수상
제일 처음 알려진 공개키 암호 중 하나
1976년, Diffie 와 Hellman 에 의해 공개키 암호 개념이 처음으로 제안됨.
1977년, Merkel 과 Hellman 에 의해 knapsack 공개키 암호시스템 제안
1984년, Adi Shamir가 다항시간 공격법을 발표
1978년, RSA 암호 발표
1973년, 영국 전자통신안전국 소속 수학자 Ellis 가 독립적으로 RSA 방식의 암호를 먼저 개발하였으나 1997년에 비로소 이러한 사실이 공개
현재까지 상용 시스템에 널리 사용되고 있음
Secure web communication (SSL/TLS), Authorized certificate in Korea
수학적 배경 – 𝒁𝒏
𝑍𝑛
임의의 정수를 정수 𝑛 으로 나눈 나머지들의 집합
𝑍𝑛 = {0,1 … , 𝑛 − 1}
𝑚𝑜𝑑 𝑛 덧셈, 곱셈 연산이 정의
<𝑍6 연산 테이블>
| + | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 1 | 2 | 3 | 4 | 5 |
| 1 | 1 | 2 | 3 | 4 | 5 | 0 |
| 2 | 2 | 3 | 4 | 5 | 0 | 1 |
| 3 | 3 | 4 | 5 | 0 | 1 | 2 |
| 4 | 4 | 5 | 0 | 1 | 2 | 3 |
| 5 | 5 | 0 | 1 | 2 | 3 | 4 |
| x | 0 | 1 | 2 | 3 | 4 | 5 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 |
| 2 | 0 | 2 | 4 | 0 | 2 | 4 |
| 3 | 0 | 3 | 0 | 3 | 0 | 3 |
| 4 | 0 | 4 | 2 | 0 | 4 | 2 |
| 5 | 0 | 5 | 4 | 3 | 2 | 1 |
GCD 정리
𝑎, 𝑛: 임의의 정수 & 𝑑 = gcd(𝑎, 𝑛)
⇒ 1) 𝑎𝑠 + 𝑛𝑡 = 𝑑 를 만족시키는 두 정수 𝑠, 𝑡 가 존재한다. (단, 유일하지는 않음)
2) 𝑎, 𝑛 을 위와 같은 방식으로 결합했을 때 gcd(𝑎, 𝑛) 이 얻을 수 있는 최소의 자연수이다.
(즉, 임의의 두 정수 𝑠 ′ ,𝑡′ 에 대해 |𝑎𝑠 ′ + 𝑛𝑡 ′ | ≥ 𝑑)
곱셈에 대한 역원 존재성
𝑎: 임의의 정수, 𝑛 ≥ 2: 자연수
𝑎가 𝑚𝑜𝑑 𝑛 으로 역원이 존재할 필요충분조건은 gcd 𝑎, 𝑛 = 1
- gcd 𝑎, 𝑛 = 1
- 𝑎 ⋅ 𝑠 + 𝑛 ⋅ 𝑡 = 1 인 두 정수 𝑠,𝑡 가 존재
- 위 식의 양변에 𝑚𝑜𝑑 𝑛 을 취하면, 𝑎 ⋅ 𝑠 = 1 𝑚𝑜𝑑 𝑛
- 따라서 𝑎 −1 = 𝑠 𝑚𝑜𝑑 𝑛
우리가 궁금한 문제
- gcd 𝑎, 𝑛 = 𝑑 일 때, 𝑎 ⋅ 𝑠 + 𝑛 ⋅ 𝑡 = 𝑑 인 두 정수 𝑠,𝑡 구하기
- Extended Euclidean 알고리즘으로 계산 가능
- 나눗셈을 반복적으로 수행 (기본적으로 gcd를 계산하는 과정과 같음)
- (예시) 𝑎 = 28, 𝑛 = 75 ⇒ gcd 𝑎, 𝑛 = 1 = 28 ⋅ (−8) + 75 ⋅ 3 ⇒ 28−1 = −8 = 67 (𝑚𝑜𝑑 75)
1) 28 = 0 × 75 + 28
28 = 28
2) 75 = 2 × 28 + 19
19 = −2 × 28 + 75
3) 28 = 1 × 19 + 9
9 = 28 − 19 = 28 − (−2 × 28 + 75) = 3 × 28 − 1 × 75
4) 19 = 2 × 9 + 1
1 = 19 − 2 × 9 = (−2 × 28 + 75) − 2 × (3 × 28 − 1 × 75) = −𝟖 × 𝟐𝟖 + 𝟑 × 𝟕𝟓
5) 9 = 9 × 1 + 0 ⇒ 종료 & 앞 단계 결과 반환
수학적 배경 – Group
Group의 정의
공집합이 아닌 집합 𝐺 와 𝐺의 원소에 대해 다음을 만족하는 연산 ⊗ 가 정의되면 (𝐺,⊗) 를 Group이라고 부른다
𝑎 ⊗ 𝑏 ⊗ 𝑐 = 𝑎 ⊗ (𝑏 ⊗ 𝑐)
𝑎 ⊗ 𝑒 = 𝑒 ⊗ 𝑎 = 𝑎
𝑎 ⊗ 𝑎 −1 = 𝑎 −1 ⊗ 𝑎 = 𝑒
- Abelian group
- Group (𝐺,⊗) 에서 연산⊗에 대해 교환법칙이 성립하는 경우를 말함 (𝑎 ⊗ 𝑏 = 𝑏 ⊗ 𝑎)
- Group order (위수)
- Group 𝐺의 원소의 개수, |𝐺|로 표기
- 𝐺 = ℓ (유한 위수) → 모든 𝑔 ∈ 𝐺 에 대해 𝑔^ ℓ = 1
수학적 배경 – 𝑍𝑛 ∗
𝑍𝑛 ∗
- 𝑍𝑛 의 부분집합으로 𝑍𝑛 의 원소 중에서 곱셈에 대한 역원이 존재하는 숫자들의 집합
- 정수 𝑎가 𝑍𝑛 에서 곱셈에 대한 역원이 존재 ⇔ gcd(𝑎, 𝑛) = 1
- 𝑍𝑛 ∗ ≔ {𝑎 ∈ 𝑍𝑛 ∶ gcd(𝑎, 𝑛) = 1}
- 𝑚𝑜𝑑 𝑛 곱셈에 대해 group을 형성
- 곱셈에 대한 역원은 확장 유클리드 알고리즘으로 계산
수학적 배경 – Group 𝑍𝑛 ∗
𝑍𝑛 ∗의 위수
- | 𝑍𝑛 ^∗ | = 𝜙 (𝑛)
- 모든 𝑎 ∈ 𝑍𝑛 ∗ 에 대해, 𝑎 ^𝜙(𝑛) = 1 (𝑚𝑜𝑑 𝑛)
- 오일러 정리 관점 : 𝑛 과 서로소인 정수 𝑎 에 대해, 𝑎 𝜙 𝑛 = 1 (𝑚𝑜𝑑 𝑛) 이 성립
- Group 관점 : 𝑎 ∈ 𝑍𝑛 ∗에 대해 𝑎 ^ |𝑍𝑛 ∗ | = 1 ( 𝑚𝑜𝑑 𝑛 )
수학적 배경 – RSA 암호시스템
- 소수 𝑝 & 𝑞 에 대해, 𝑛 = 𝑝𝑞 인 경우 아래가 성립
- 𝑍𝑛 ∗ 는 group
- 𝑚 ∈ 𝑍𝑛 ∗ 과 정수 𝑒에 대해, 𝑍𝑛 ∗ 에서 거듭제곱 𝑚^𝑒 이 잘 정의됨 (𝑚𝑜𝑑 𝑛 곱셈 연산)
- |𝑍𝑛 ∗| = 𝜙 (𝑛) = 𝜙 (𝑝 ⋅ 𝑞) = (𝑝 − 1) ⋅ (𝑞 − 1)
- 모든 𝑚 ∈ 𝑍𝑛 ∗ 에 대해 𝑚^|𝑍𝑛 ∗ | = 𝑚^𝜙(𝑛) = 1 (𝑚𝑜𝑑 𝑛)
- 모든 𝑚 ∈ 𝑍𝑛 ∗ 에 대해 𝑚^𝑒 = 𝑚^𝑒 𝑚𝑜𝑑 |𝑍𝑛 ∗ | = 𝑚^𝑒 (𝑚𝑜𝑑 𝜙 𝑛 )
- 즉, 𝑍𝑛 ∗ 에서 거듭제곱을 하는 경우, 지수를 0 ≤ 𝑒 (𝑚𝑜𝑑 𝜙(𝑛)) < 𝜙 𝑛 로 두고 계산하면 됨
- gcd 𝑒, 𝜙(𝑛) = 1 인 경우를 생각
- GCD 정리에 의해 𝑒 는 𝑚𝑜𝑑 𝜙 (𝑛) 에 대해 곱셈 역원을 가짐
- 즉, 𝑒 ⋅ 𝑑 = 1 (𝑚𝑜𝑑 𝜙 (𝑛) ) 인 1 ≤ 𝑑 < 𝜙 (𝑛) 이 존재
- 위 숫자 𝑒, 𝑑 에 대해 아래가 성립
- (𝑚^𝑒)^𝑑 = 𝑚^𝑒𝑑 = 𝑚^𝑒𝑑 (𝑚𝑜𝑑 𝜙 (𝑛) ) = 𝑚 (𝑚𝑜𝑑 𝑛)
- RSA에서 𝑚 이 메시지, 𝑒 가 공개키, 𝑑 가 개인키가 된다
- 암호화 : 𝑐 = 𝑚^𝑒 (𝑚𝑜𝑑 𝑛)
- 복호화 : 𝑐 ^𝑑 = (𝑚^𝑒) ^𝑑 = 𝑚^𝑒𝑑 = 𝑚^𝑒𝑑 ^(𝑚𝑜𝑑 𝜙(𝑛) ) = 𝑚 (𝑚𝑜𝑑 𝑛)
RSA 키 생성
- B가 아래의 순서로 공개키/개인키를 생성
- 두 개의 큰 소수 𝑝, 𝑞 를 random하게 생성
- RSA modulus 𝑛 을 𝑛 = 𝑝 ⋅ 𝑞 로 setting
- 공개키 𝑒 생성
- gcd(𝑒,𝜙 𝑛 ) = 1 을 만족하는 1 < 𝑒 < 𝜙(𝑛)
- 개인키 𝑑 생성
- 𝑒 ⋅ 𝑑 = 1 𝑚𝑜𝑑(𝜙 𝑛 ) 이 되는 𝑑 를 확장 유클리드 알고리즘으로 계산
- (𝑛, 𝑒) 를 공개하고, (𝑝, 𝑞, 𝑑) 는 개인키로 보관
RSA 암호화 알고리즘
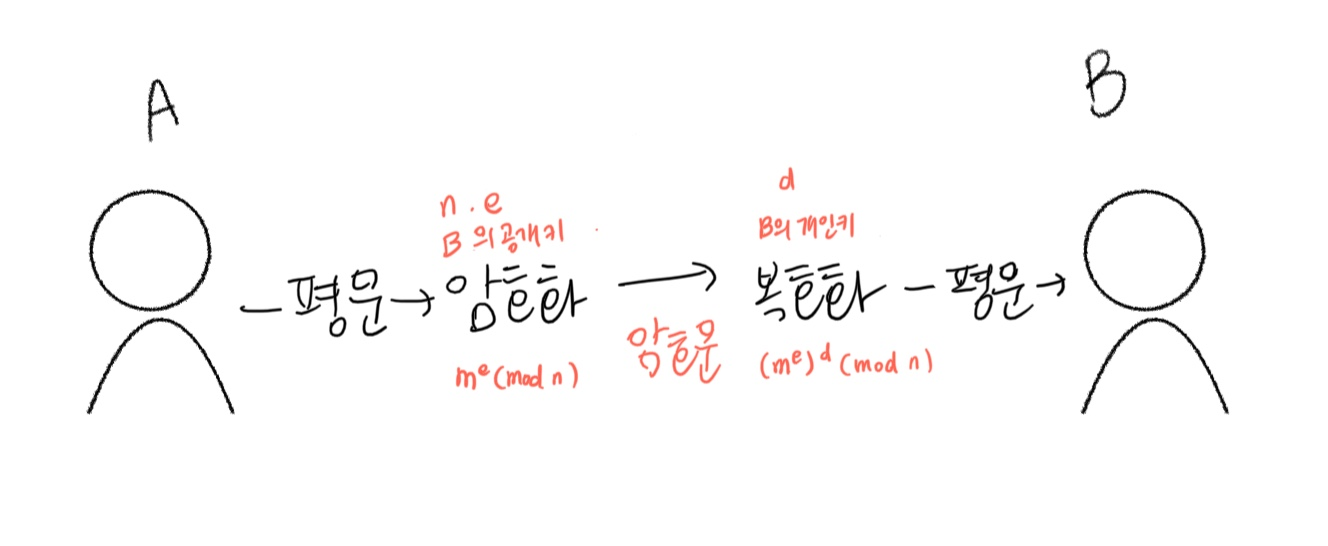
암호화
- A 가 아래와 같이 암호화하여 B 에게 전송
- A 가 보낼 메시지 0 ≤ 𝑚 < 𝑛
- B 의 공개키 𝑒 에 대해
- 𝑐 = 𝑚𝑒 (𝑚𝑜𝑑 𝑛)
- 암호문 𝑐 를 B에게 전송
RSA 복호화 알고리즘
복호화
- B 가 아래와 같이 복호화를 수행
- A로 부터 받은 암호문 𝑐 = 𝑚^𝑒 (𝑚𝑜𝑑 𝑛)
- B 의 개인키 𝑑 에 대해,
- 𝑐^𝑑 = (𝑚^𝑒) ^𝑑
- = 𝑚^𝑒𝑑
- = 𝑚^𝑒𝑑 ^(𝑚𝑜𝑑 𝜙 𝑛 )
- = 𝑚 (𝑚𝑜𝑑 𝑛)
RSA 복호화 알고리즘이 작동하는 이유
- 𝑚 ∈ 𝑍𝑛 ∗ 인 경우
- 앞에서 보았던 과정(수학적 배경)에 따라
- (𝑚^𝑒)^𝑑 = 𝑚^𝑒𝑑 = 𝑚^𝑒𝑑 ^(𝑚𝑜𝑑 𝜙 𝑛 ) = 𝑚 (𝑚𝑜𝑑 𝑛) 이 성립
- 앞에서 보았던 과정(수학적 배경)에 따라
- 𝑚 이 𝑍𝑛 의 원소 이지만, 𝑍𝑛 ∗ 의 원소는 아닌 경우
- 즉, gcd 𝑚, 𝑛 ≠ 1 인 경우
- (case 1) 𝑚 = 0 인 경우
- 𝑐 = 0^𝑒 = 0(𝑚𝑜𝑑 𝑛) ⇒ 𝑐^𝑑 = 0 ^𝑑 = 0 (𝑚𝑜𝑑 𝑛) 으로 잘 복호화 된다
- (case 1) 𝑚 이 𝑝 의 배수이고, 𝑚 이 𝑞 의 배수가 아닌 경우
- 𝑚 = 𝑘𝑝, 𝑞 ∤ 𝑚
- 𝑝, 𝑞 각각에 대해 배수 관계를 분석하면 잘 복호화 됨을 확인할 수 있음 (강의 범위 외)
빠른 지수승 연산
- RSA 공개키 암호시스템에서 암/복호화는 지수승 연산을 수행
- 𝑚^𝑒 (𝑚𝑜𝑑 𝑛), 𝑐^ 𝑑 (𝑚𝑜𝑑 𝑛)
- 1 < 𝑒, 𝑑 < 𝜙 𝑛 = 𝑝 − 1 ⋅ (𝑞 − 1) → 𝑛 과 거의 비슷한 크기
- n 는 수천 비트 숫자
- 단순한 계산법
- 𝑐^𝑑 = 𝑐 × 𝑐 × ⋯ × 𝑐 (𝑚𝑜𝑑 𝑛) → 𝑑 − 1 번 곱하기
- 𝑑 가 60비트 숫자라고만 해도 약 2 ^ 60 번 곱하기 필요
- 현실적으로 불가능한 계산
- 𝑐 ∈ 𝑍𝑛 와 0 < 𝑑 < 𝜙(𝑛) 에 대해, 𝑐 𝑑 을 빠르게 계산하기
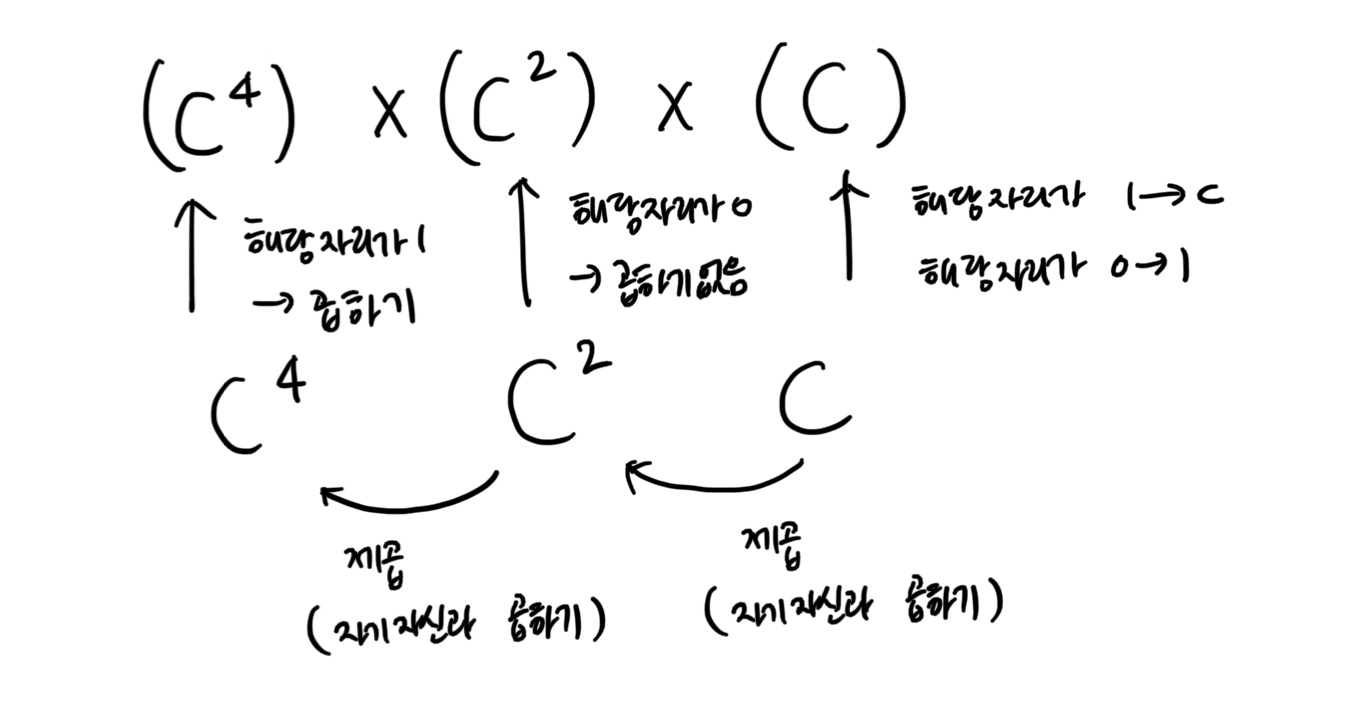
- Square & Multiply (exponentiation by squaring)
- 약 2 log 𝑑 번 곱셈으로 지수승 연산 (60 vs 2 ^60 )
- 𝑐 𝑑 에서 𝑑 를 이진수로 표현 𝑑 = (𝑑59, … , 𝑑0)
- 비트 별로 읽어가면서 제곱 및 곱하기 연산을 통해 계산
- 간단한 예 𝑐 ^5 = 𝑐 ^1012 = 𝑐^1002 × 𝑐 ^12 = (𝑐^4)^1 × (𝑐^ 2)^ 0 ×(𝑐)^1
📌RSA 암호 안전성
공격자 모델 리뷰
3주차_ 현대암호학 기초 < 암호 안전성과 공격 모델 > (tistory.com)
3주차_ 현대암호학 기초 < 암호 안전성과 공격 모델 >
목차는 아래와 같다. 안전한 암호 시스템 암호 공격자 모델 📌 안전한 암호 시스템 공격자가 암호화/복호화 키를 계산해 낼 수 없으면 안전한 알고리즘이다? 키 복구 공격을 하지 못하지만 안전
jootopia0808.tistory.com
공개키 암호가 기본적으로 고려해야 하는 공격자 모델
- 공개키 암호에서는 공격자가 임의의 메시지에 대해 암호문을 생성할 수 있다
- 즉, 공격자는 선택 평문 공격 (CPA) 이 항상 가능하다
- RSA의 경우
- 공개키 𝑛, 𝑒 는 누구에게나 공개
- 공격자가 임의의 메시지 𝑚 에 대해 암호문 𝑐 = 𝑚𝑒 (𝑚𝑜𝑑 𝑛) 을 생성할 수 있음
- 따라서 공개키 암호는 기본적으로 CPA에 안전하게 설계하는 것이 필요
공개키 암호에 대한 중간자 공격
- 공개키 암호의 가장 큰 문제점
- 공개된 공개키가 진짜 공개키 주인의 것인지 확인할 방법이 없음
- 중간자 공격
- C가 A 에게는 스스로를 B라고 하며 A에게 자신의 공개키를 공개
- C가 B 에게는 스스로를 A라고 하며 B에게 자신의 공개키를 공개
- A 와 B 는 각각 상대방과 암호화 통신을 하고 있다고 생각하지만, 사실은 C가 중간에서 모든 통신을 들여 다보고 있는 상황이 발생
- 공개키 주인을 인증하는 시스템이 필요 → 공개키 인증서
RSA 암호 안전성 기반 문제
- RSA 암호 안전성은 아래 3가지 문제를 고려하는 것이 필요함
- 즉, RSA 암호 안전성은 아래 3 문제가 어렵다는 가정하에 보장됨
RSA 문제
공개키 (𝑛 = 𝑝 ⋅ 𝑞, 𝑒) 와 암호문 𝑐 = 𝑚^𝑒 (𝑚𝑜𝑑 𝑛) 가 주어졌을 때, 𝑚 을 찾는 문제
RSA 비밀키 문제
공개키 (𝑛 = 𝑝 ⋅ 𝑞, 𝑒) 가 주어졌을 때, 개인키 𝑑 를 계산하는 문제
인수분해 문제
두 개의 random한 큰 prime 𝑝, 𝑞 에 대해 𝑛 = 𝑝 ⋅ 𝑞 가 주어졌을 때, 𝑛 을 소인수분해하여 𝑝, 𝑞 를 계산하는 문제
RSA 암호 안전성 기반 문제 간의 관계
RSA 문제
공개키 (𝑛 = 𝑝 ⋅ 𝑞, 𝑒) 와 암호문 𝑐 = 𝑚^𝑒 (𝑚𝑜𝑑 𝑛) 가 주어졌을 때, 𝑚 계산
RSA 비밀키 문제
공개키 (𝑛 = 𝑝𝑞, 𝑒) 가 주어졌을 때, 개인키 𝑑 계산
인수분해 문제
𝑛 = 𝑝𝑞 가 주어졌을 때, 𝑝 와 𝑞 계산
- 인수분해 문제를 해결할 수 있으면, RSA 비밀키 문제와 RSA 문제를 해결할 수 있다
- 빠른 인수분해 알고리즘이 있는 경우 𝑛 → 𝑝, 𝑞 계산
- 𝑝, 𝑞 를 알면 𝜙 (𝑛) = (𝑝 − 1) (𝑞 − 1) 계산 → 𝑑 = 𝑒^ −1 (𝑚𝑜𝑑 𝜙 (𝑛)) 계산 → RSA 비밀키 문제 해결
- 𝑑 를 알기 때문에 𝑚 = 𝑐^𝑑 (𝑚𝑜𝑑 𝑛) 으로 RSA 문제 해결
- 인수분해 문제를 해결할 수 있으면, RSA 비밀키 문제와 RSA 문제를 해결할 수 있다
- RSA 비밀키 문제를 해결할 수 있으면, 인수분해 문제를 해결할 수 있다 (Alexander May, 2004)
- 즉, 인수분해 문제가 어려우면, RSA 비밀키는 공개키로부터 계산할 수 없다
- 결론적으로, 인수분해 문제와 RSA 비밀키 문제는 동치
- 인수분해 문제를 해결할 수 있으면, RSA 비밀키 문제와 RSA 문제를 해결할 수 있다
- RSA 비밀키 문제를 해결할 수 있으면, 인수분해 문제를 해결할 수 있다 (Alexander May, 2004)
- RSA 문제를 해결할 수 있으면, 인수분해 문제를 해결할 수 있는지 여부는 아직 알려지지 않음
- 즉, 현재까지 인수분해 문제와 관련해서 우리가 이야기할 수 있는 것
- 인수분해 문제가 어렵기 때문에, 공개키가 공개되더라도 개인키는 안전하다? → 참
- 인수분해 문제가 어렵기 때문에, 암호문으로부터 평문을 복구할 수 없다? → 아직 모르기 때문에 거짓
- 다만, 많은 사람들이 위 명제가 참일 것이라 믿고 있음
인수분해의 어려움
- RSA Factoring challenge
- RSA Security LLC 에서 1991년 ~ 2007년까지 운영한 인수분해 경진대회
- 문제로 RSA modulus 𝑛 을 제시하고, 소인수분해에 성공한 팀에게 상금을 지급
- 현실적으로 인수분해 능력이 어디까지 왔고, 그래서 어떤 크기의 𝑛 이 사용되어야 하는지를 가늠해볼 수 있는 대회
RSA 파라미터 선택
- 미국 국립표준연구소 (NIST) 가이드라인 (SP800-57 문서에서 제시)
- 1024 비트 𝑛 은 신규용도로 사용하지 않는다
- 2048 비트 𝑛 은 2030 년 까지 신규용도로 사용할 수 있다
- 4096 비트 𝑛 은 2031년 이후에도 신규 용도로 사용가능 하다
- AES 키 길이와 RSA 키 길이 비교
| AES | RSA |
| 128 비트 키 | 3072 비트 n |
| 192 비트 키 | 7680 비트 n |
| 256 비트 키 | 15360 비트 n |
- 현실에서 새로운 시스템 기준으로 2048 비트 RSA modulus 𝑛 을 주로 사용
- 소수 𝑝, 𝑞 생성
- 두 소수의 크기가 비슷하면서도, 𝑝 − 𝑞 값의 차이가 크도록
- 𝑝 − 1 과 𝑝 + 1 각각이 큰 소수 약수를 가지도록
- 일반적으로 random하게 생성하면 위 성질을 만족함
- 공개키 𝑒 선택
- 보통 암호화 연산 효율화를 위해 𝑒 = 2 ^ 16 + 1 = 65537 을 사용
- 사용자 모두에 대해 𝑒 는 같더라도, 𝑛 이 각자 다르므로 𝑑 도 각자 다름
Textbook RSA의 문제점
- Textbook RSA는 결정론적 암호화 알고리즘
- 𝑐 = 𝑚𝑒 (𝑚𝑜𝑑 𝑁)
- 같은 메시지에 대한 암호문이 항상 같다
- 직관적 공격 방법 (공격자의 전략)
- 가능한 평문에 대한 암호문을 생성
- 이후에 받은 암호문이 위에 생성한 암호문들 중에서 같은 것이 있는 경우 평문을 알 수 있음
- “Textbook RSA는 사용되지 않음
RSA OAEP
- OAEP (Optimal Asymmetric Encryption Padding)
- 결정론적 공개키 암호시스템을 비결정론적 공개키 암호시스템으로 변환하는 메커니즘을 제공
- 같은 메시지에 대해서도 다른 암호문이 생성되도록 함
- Bellare와 Rogaway에 의해 제안 (1994)
- 공개키 암호 표준 PKCS#1 으로 상용화되어 사용 중
- 즉, 우리가 실제로 사용하는 RSA는 RSA-OAEP
- 선택 암호문 공격 (CCA) 에도 안전함이 증명되어 있음
- 핵심 아이디어
- RSA 메시지 파트에 random 비트열을 추가
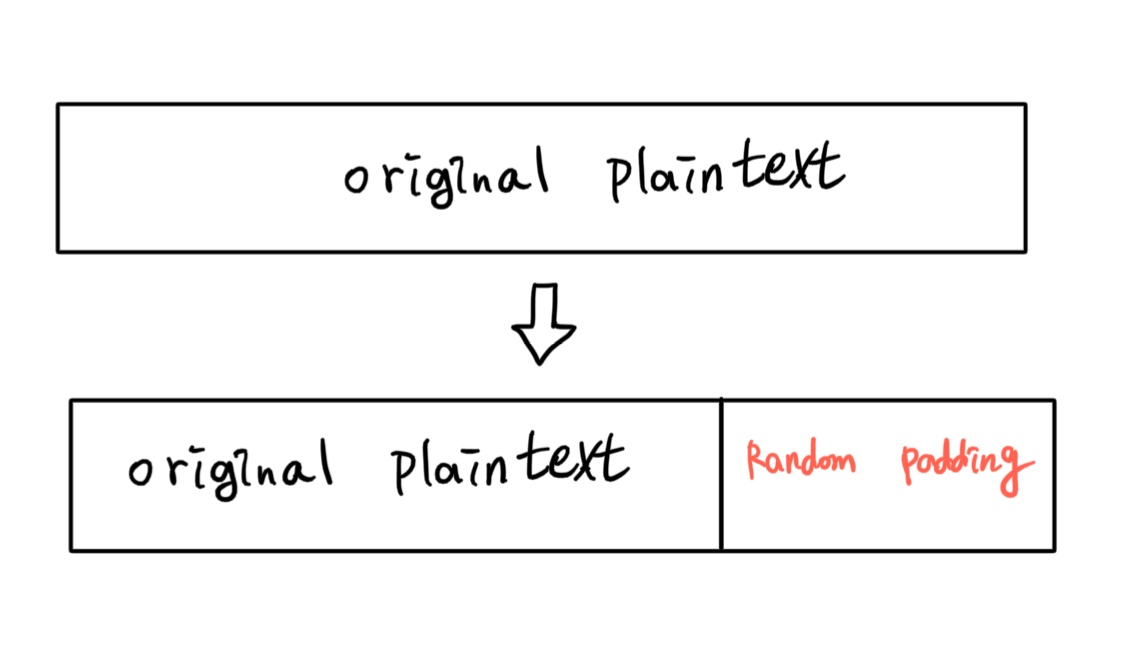
- Random padding으로 인해 같은 평문에 대한 암호문이 항상 달라짐
'SWU_1학년 2학기 > 현대 암호학 기초' 카테고리의 다른 글
| 10주차_현대암호학 기초 [기초 대수학] (0) | 2023.11.14 |
|---|---|
| 9주차_현대암호학 기초 [ 블록 암호 모드(Mode of Operation) ] (0) | 2023.11.05 |
| 4주차_현대암호학 기초 (2) | 2023.10.08 |
| 3주차_ 현대암호학 기초 < 암호 안전성과 공격 모델 > (1) | 2023.10.01 |
| 3주차_현대암호학 기초 < 고전 암호 > (2) | 2023.10.01 |