2024. 11. 13. 13:22ㆍAlgorithm ( p & swlug )/Baekjoon
문제
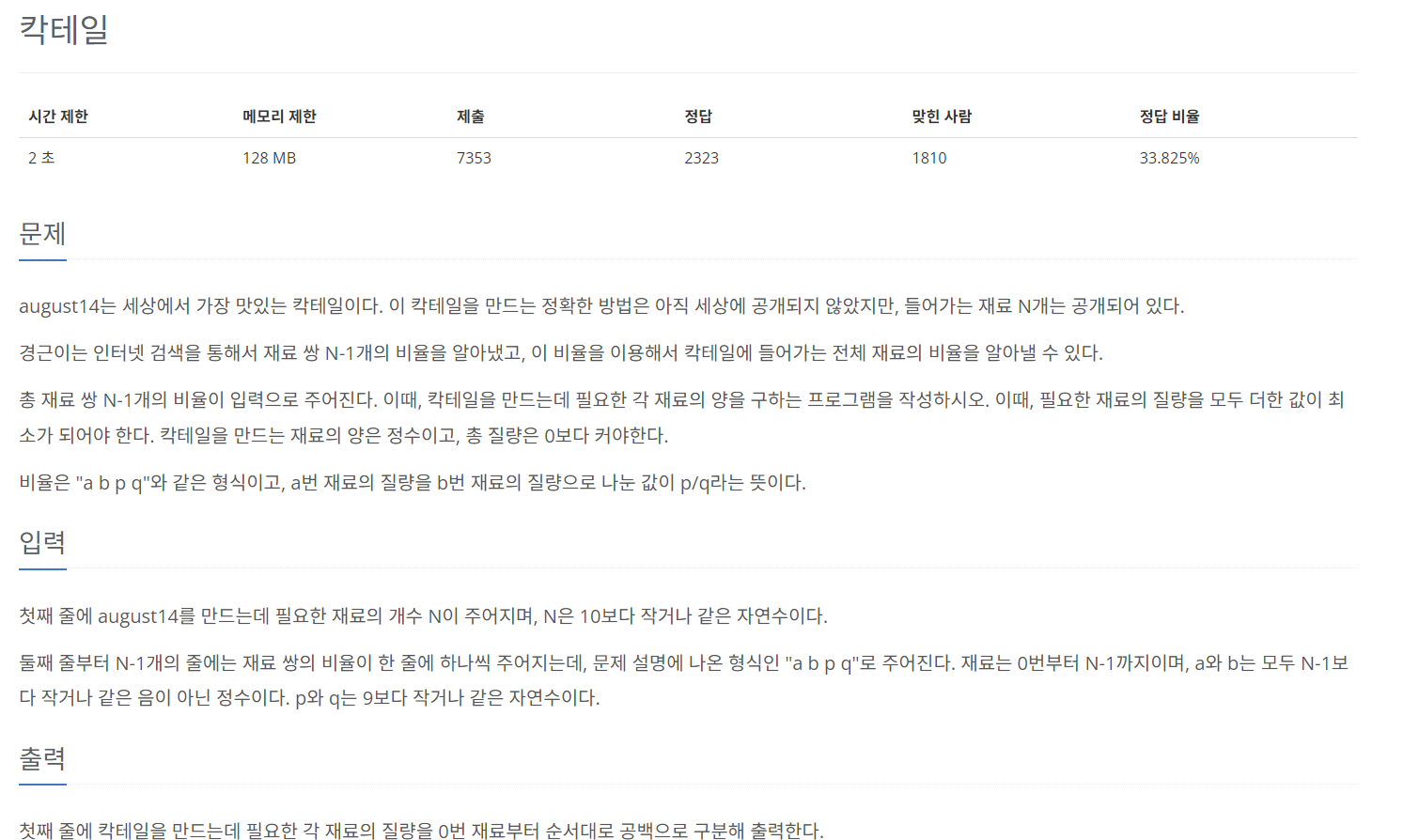
august14는 세상에서 가장 맛있는 칵테일이다. 이 칵테일을 만드는 정확한 방법은 아직 세상에 공개되지 않았지만, 들어가는 재료 N개는 공개되어 있다.
경근이는 인터넷 검색을 통해서 재료 쌍 N-1개의 비율을 알아냈고, 이 비율을 이용해서 칵테일에 들어가는 전체 재료의 비율을 알아낼 수 있다.
총 재료 쌍 N-1개의 비율이 입력으로 주어진다. 이때, 칵테일을 만드는데 필요한 각 재료의 양을 구하는 프로그램을 작성하시오. 이때, 필요한 재료의 질량을 모두 더한 값이 최소가 되어야 한다. 칵테일을 만드는 재료의 양은 정수이고, 총 질량은 0보다 커야한다.
비율은 "a b p q"와 같은 형식이고, a번 재료의 질량을 b번 재료의 질량으로 나눈 값이 p/q라는 뜻이다.
입력
첫째 줄에 august14를 만드는데 필요한 재료의 개수 N이 주어지며, N은 10보다 작거나 같은 자연수이다.
둘째 줄부터 N-1개의 줄에는 재료 쌍의 비율이 한 줄에 하나씩 주어지는데, 문제 설명에 나온 형식인 "a b p q"로 주어진다. 재료는 0번부터 N-1까지이며, a와 b는 모두 N-1보다 작거나 같은 음이 아닌 정수이다. p와 q는 9보다 작거나 같은 자연수이다.
출력
첫째 줄에 칵테일을 만드는데 필요한 각 재료의 질량을 0번 재료부터 순서대로 공백으로 구분해 출력한다.
📌문제풀이 (내생각)
세상에서 가장 맛있는 칵테일인 august14를 만들고자, 각 재료의 비율을 계산하기 위해서는 전체 비율을 표현할 수 있는 최소 단위를 찾아야할텐데 이를 풀기위해서 재료 간의 비율을 유지하면서, 각 재료의 최종 양을 자연수로 만들어야 하므로 비율의 분모들을 모두 포함하는 최소 공배수를 찾아야할 것 같다.
📌 코드 분석
import sys
input = sys.stdin.readline
n = int(input())
ratio = [[] for _ in range(n)]
mass = [0] * (n)
visited = [False] * n
## 유클리드 호제법 함수
def gcd(a,b):
if a%b == 0:
return b
return gcd(b,a%b)
##관계리스트 생성
common_multi = 1
for _ in range(n-1):
a, b, p, q = map(int,input().split())
ratio[a].append((b,p,q))
ratio[b].append((a,q,p))
common_multi *= ((p*q)//gcd(p,q))
mass[0] = common_multi
##비율에 맞춰 계산하기 위한 그래프 탐색
def DFS(r):
visited[r] = True
for i in ratio[r]:
if not visited[i[0]]:
mass[i[0]] = i[2] * mass[r] // i[1]
DFS(i[0])
DFS(0)
##최대 공약수 구하기
greatest_common_divisor = mass[0]
for i in range(n):
greatest_common_divisor = gcd(greatest_common_divisor,mass[i])
##최대공약수로 각 질량을 나눠줌
for i in range(len(mass)):
mass[i] = mass[i] // greatest_common_divisor
print(*mass)
- n은 재료의 개수
- ratio는 각 재료와 다른 재료 간의 비율 관계를 저장하기 위한 리스트로, 각 인덱스에 연결된 (재료 번호, 비율 p, 비율 q) 형식의 튜플이 저장된다.
- mass는 각 재료의 최종 질량을 저장할 리스트이다.
- visited는 각 재료가 이미 방문되었는지를 확인하기 위한 리스트이다.
- 유클리드 호제법을 이용해 두 수 a와 b의 최대 공약수를 계산하는 재귀 함수이다.
- gcd는 비율의 분모와 분자를 나눌 때, 그리고 최종 질량에서 공통된 약수를 제거할 때 사용된다.
- 각 재료의 관계 (a와 b가 p비율로 연결된 관계)를 ratio에 저장한다.
- 동시에 p와 q의 최소 공배수를 계산하여 common_multi에 곱하며, 이 값은 각 재료의 비율을 계산하기 위한 공통 최소 단위를 의미한다.
- 마지막으로 mass[0]에 common_multi를 할당하여 첫 번째 재료의 기본 질량을 설정한다.
유클리드 호제법을 사용하는 것은 최소공배수를 위해 사용할 수 있는 하나의 방법이다.
- DFS(깊이 우선 탐색)을 사용하여 재료 r을 기준으로 연결된 재료들의 비율에 맞춰 질량을 할당한다다.
- mass[i[0]] = i[2] * mass[r] // i[1]를 통해 현재 재료 r의 질량을 비율에 맞춰 연결된 재료의 질량을 계산하고 mass에 저장한다.
- 재료마다 visited를 통해 방문 여부를 확인하고, 재귀적으로 모든 재료에 대한 질량을 계산한다.
- mass에 저장된 각 재료의 질량에 대해 공통된 최대 공약수(GCD)를 구하여 greatest_common_divisor에 저장한다.
- 각 질량을 최대 공약수로 나눔으로써 최종적으로 각 재료의 최소 정수 비율을 유지하면서 정수 질량을 계산한다.
- 최종 결과로 mass의 모든 요소를 출력한다.
📌 느낀점
해당 문제는 생각보다 많은 자료구조를 요구하고 유클리드호제법까지도 활용하면 좋을 문제라서 높은 수준의 알고리즘이라고 느껴졌다.
기초적인 알고리즘의 수준을 좀 끌어올린다면 풀어보기 좋은 문제라고 생각한다.
[ 참고 자료 ]
[백준 1033번] 칵테일 (Python/파이썬) — Codio: 컴퓨터 학부생의 인생이야기
[백준 1033번] 칵테일 (Python/파이썬)
https://www.acmicpc.net/problem/1033 1033번: 칵테일 august14는 세상에서 가장 맛있는 칵테일이다. 이 칵테일을 만드는 정확한 방법은 아직 세상에 공개되지 않았지만, 들어가는 재료 N개는 공개되어 있다.
codio.tistory.com
'Algorithm ( p & swlug ) > Baekjoon' 카테고리의 다른 글
| 2학년 2학기 알고리즘 과제_6주차(백준_1074번:Z) (0) | 2024.11.16 |
|---|---|
| 2학년 2학기 알고리즘 과제_5주차(백준_1063번:킹) (0) | 2024.11.13 |
| 2학년 2학기 알고리즘 과제_4주차(백준_24511번:queuestack) (2) | 2024.11.06 |
| 2학년 2학기 알고리즘 과제_4주차(백준_2346번:풍선 터뜨리기) (0) | 2024.11.06 |
| 2학년 2학기 알고리즘 과제_3주차(백준_1051번:숫자 정사각형) (0) | 2024.10.30 |